Coin Change, Dynamic Programming

DSA#0 in Rust

Hi Guys, I'm Starting a new series of solving DSA problems on Rust. Why? Because I am learning Rust and DSA, what better way, than to write about it?

Question

You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money.

Return the fewest number of coins that you need to make up that amount. If any combination of the coins cannot make up that amount of money, return -1.

You may assume that you have an infinite number of each kind of coin.

Let’s get into it …

You are given an array of Integers representing the denominations of a particular currency. And a total amount Sum. Return the minimum number of combinations required to make up that sum … blah ..blah ..blah.

So after a few hours of thinking, I finally looked up the answer on the web and found that there are two popular approaches to solve this problem.

1. Greedy Algorithm

2. Dynamic programming

Approach 1

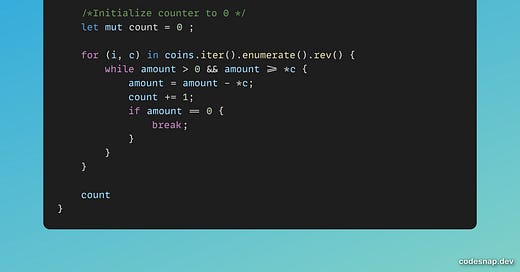
I implemented the Greedy Algorithm and let me explain my code and what I am trying to do here.

The idea is to start with a sorted vector of integers. Why? Because then we can start with the highest denomination. Well, that makes sense !!

For example:

If our denominations are [3, 7, 1 ] and the target amount is 12 then we can sort it to get [1, 3, 7,] and then get a combination 7+3+1+1 which will be the minimum number of coins required.

Then we iterate over the vector from the end (reverse iteration) and subtract the sum with the denomination as long the result is not equal to zero and the selected element is less than or equal to the remaining amount [don’t forget to update the counter]. If it is greater than the remaining amount drop down to the next element to the left.

Well, I thought this would do the trick but it didn’t. It does not solve all the test cases.

To solve this we shift to the dynamic programming approach.

Approach 2

Here we initialise a dp vector which will have amount+1 elements and all initialised to amount + 1. For each element in the DP, we find the minimum number of denominations required to get the target amount.

So after a day of trying to understand both approaches, I finally completed the first post of the DSA series.

Drop a like or comment on a better approach to the problem.